面向最小哈希签名的LSH

LSH

我们知道最小哈希签名能够把一篇较大的文档压缩成一个较短的签名并且不影响文档间的Jaccard相似度。很多情况下，我们用最小哈希签名的目的就是为了方便的对文档进行存储，并且对于给定的文档，能在大量的文档中快速的查找相似的文章。现在我们能做到快速的对两篇文章进行相似度比较，但是当总的文档数目比较大的时候，比较所有文档的最小哈希签名仍然是一个非常耗时耗力的事。而我们知道，对于给定的文档而言，文档库中的绝大多数文档其实都没有比较的意义，如果能有一个方法能过滤掉不需要比较的大量文档，那么显然就能加快整个查找的过程。这个思路其实可以称为"Filter and Refine"，"先过滤，后提纯"。而实现这个的方法，就是LSH(Locality-Sensitive Hashing 局部敏感哈希)。

现在先不精确定义LSH，只要知道LSH是一种对大量数据进行过滤的方法即可。

面向最小哈希签名的LSH

对于最小哈希签名来说，我们可以通过一种叫“行条化策略”的方法，对最小哈希签名再进行一次哈希。怎么做呢？

对于$n$个长度为$k$的最小哈希签名的集合$S_1,S_2,S_3,...,S_n$、以及生成他们的的$k$个哈希函数来说，我们用下面的签名矩阵来表示他们：
$$
\begin{matrix}&S_1&S_2&S_3&...&S_n\\h_1&x&x&x&x&x\\h_2&x&x&x&x&x\\h_3&x&x&x&x&x\\...&x&x&x&x&x\\h_k&x&x&x&x&x\\\end{matrix}
$$

其中一列就表示一个最小哈希签名。

接着，我们把这个矩阵平均划分成$b$个行条，每个行条有$r$行(显然$r*b=k$)。这相当于我们把每一个签名分成了$b$段，每一段有$r$个数。然后我们再分别对每一段进行一次哈希，将该段相同的哈希签名放在一个桶中，该段不同的放在不同的桶中(当然，不同行条的桶互不影响）。这就相当于把一个长度为$k$的最小哈希签名映射到了$b$个桶中。

这样一来，我们如果我们需要对某个最小哈希签名进行相似查找，我们只要对这$b$个桶中的那些东西进行比较即可，省去了很多不必要的比较。

行条化策略分析

那么用行条化策略后会不会影响我们查询的准确性呢？答案是---当然会。

所谓影响正确性，无非就两种，一种是伪正例(false positive)，一种是伪反例(false negative)。

所谓伪正例，就是指我们把不相似的签名加到了进一步比较的列表中。对于伪正例而言，我们显然不用担心，因为下一步直接比较的目的就是去除伪正例，只是会害我们多比较几次，因此我们主要关注的是伪反例。

所谓伪反例，就是指我们把相似度很高的签名给漏掉了。这就很尴尬了，因为漏掉的话以后就再也不会考虑到他了。这是我们需要极力避免的。

那么伪反例的比例到底是怎么样的呢？

我们知道在两个签名的Jaccard相似度为$s$的情况下，这两个签名的某一个位相等的概率就是$s$，那么在某一行相等的概率就是$s^r$，那么在任意一行都不相等的概率就是$(1-s^r)^b$，那么他们最终成为候选对的概率就是$(1-(1-s^r)^b)$。也就是说两个签名最终会被放在一起作为进行比较的概率$P=1-(1-s^r)^b$。

也就是说，对于给定的$s\ r\ b$，伪反例的比例就是$1-P$。假设$s=0.8,b=20,r=5$，这时伪反例的比例就是0.000356，还是相当低的，而且随着b的增大，这个值还会变得更小。

接下来我们就分析以下如何根据我们需要的$s$来确定参数$r,b$。不管$r,b$的取值是什么，$P$关于$s$的函数图像基本是这样的：

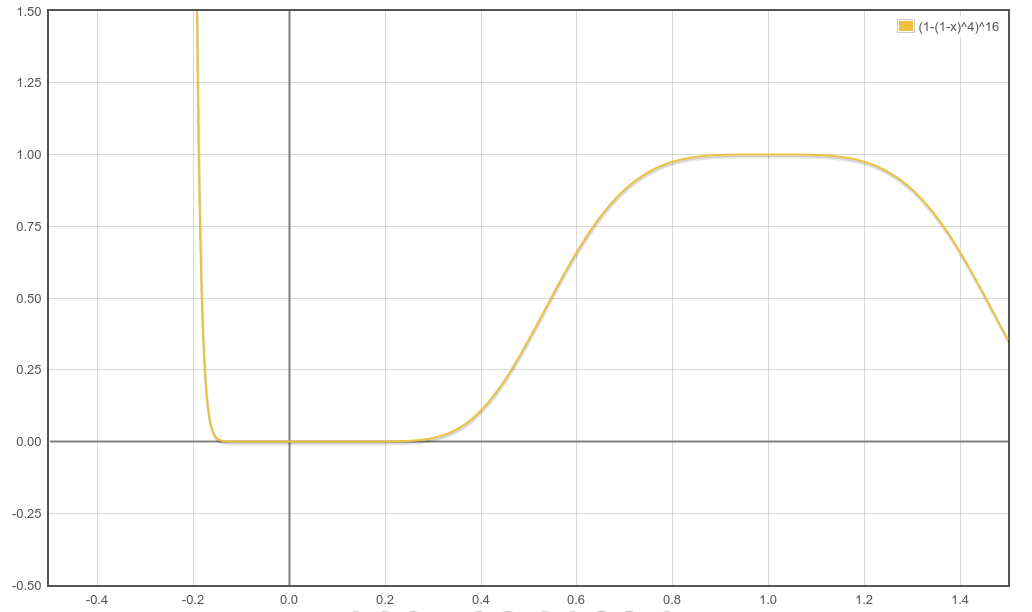
注意到$s$的取值在0到1之间，这个函数图像和sigmoid还是有点像的，虽然突变的部分不是很明显，但是还是两端的差距还是很明显的。通过调节这个函数的参数，我们就可以控制只把相似度大于一定阈值$s_{thresh}$的签名以很高的概率纳为候选对，而相似度低的签名以很低的概率不纳为候选对。通常情况下我们会通过调节$r,b$，使这个阈值$s_{thresh}$对应到概率为0.5的地方，这个时候就有$s_{thresh}=(1-2^{-\frac 1b})^{\frac 1r}$。不过有时候为了方便，也为了更准确，这个$s_{thresh}$会设置为$(\frac 1b)^{\frac 1r}$。当$s=(\frac 1b)^{\frac 1r}$时，我们可以算出来，概率$Q=1-(1-\frac 1b)^b$。显然$\underset{b\to \infty}{Q}\to 1-\frac1e\approx 0.632$。也就是说这个值会比0.5稍大，不过实际上效果可能更好。